What are graphs?
A graph is a non-linear kind of data structure made up of nodes or vertices and edges. The edges connect any two nodes in the graph, and the nodes are also known as vertices.
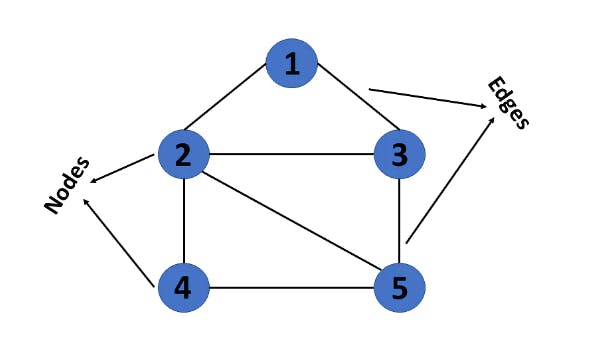
This graph has a set of vertices V= {1,2,3,4,5} and a set of edges E= { (1,2),(1,3),(2,3),(2,4),(2,5),(3,5),(4,50 }.
Types of graphs
1. Finite Graph
The graph G=(V, E) is called a finite graph if the number of vertices and edges in the graph is limited in number.
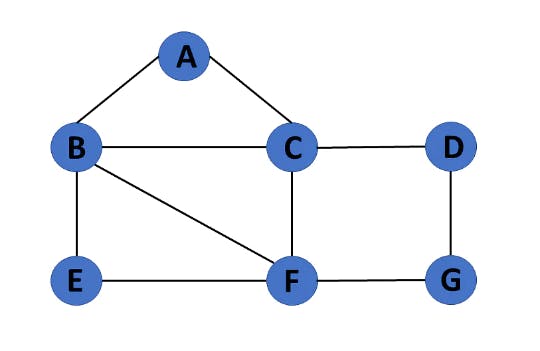
2. Infinite Graph
The graph G=(V, E) is called a finite graph if the number of vertices and edges in the graph is interminable.
3. Trivial Graph
A graph G= (V, E) is trivial if it contains only a single vertex and no edges.

4. Simple Graph
If each pair of nodes or vertices in a graph G=(V, E) has only one edge, it is a simple graph. As a result, there is just one edge linking two vertices, depicting one-to-one interactions between two elements.
5. Multi Graph
The graph is referred to as a multigraph if there are numerous edges between a pair of vertices in a graph G= (V, E). There are no self-loops in a Multigraph.
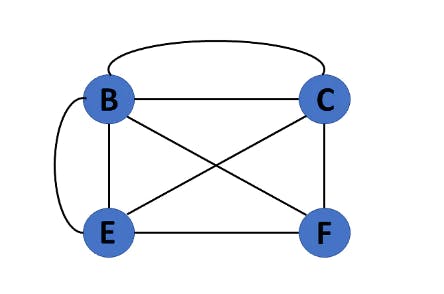
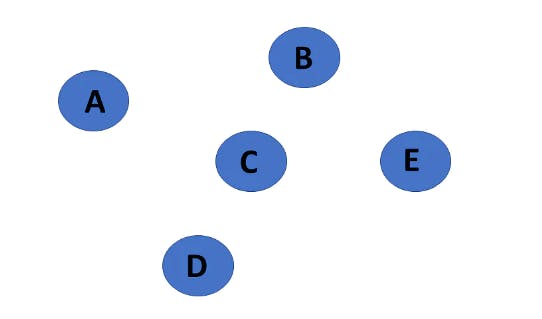
6. Null Graph
It's a reworked version of a trivial graph. If several vertices but no edges connect them, a graph G= (V, E) is a null graph.
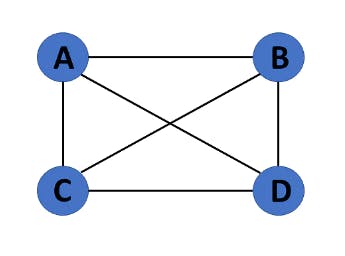
7. Complete Graph
If a graph G= (V, E) is also a simple graph, it is complete. Using the edges, with n number of vertices must be connected. It's also known as a full graph because each vertex's degree must be n-1.
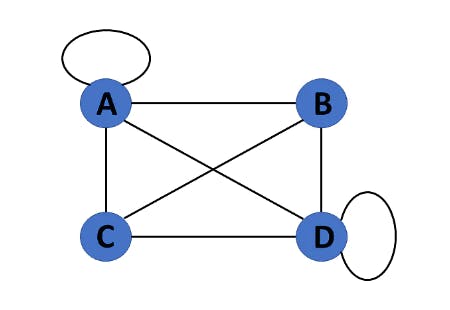
8. Pseudo Graph
If a graph G= (V, E) contains a self-loop besides other edges, it is a pseudograph.
9. Regular Graph
If a graph G= (V, E) is a simple graph with the same degree at each vertex, it is a regular graph. As a result, every whole graph is a regular graph.
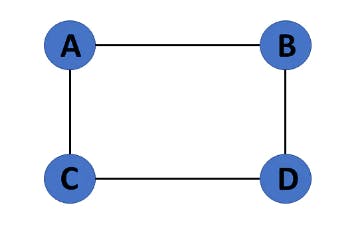
10. Weighted Graph
A graph G= (V, E) is called a labeled or weighted graph because each edge has a value or weight representing the cost of traversing that edge.
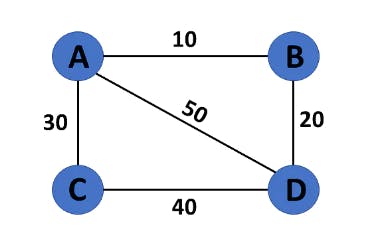
11. Directed Graph
A directed graph also referred to as a digraph, is a set of nodes connected by edges, each with a direction.
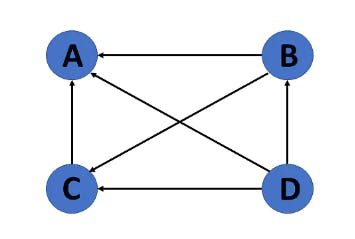
12. Undirected Graph
An undirected graph comprises a set of nodes and links connecting them. The order of the two connected vertices is irrelevant and has no direction. You can form an undirected graph with a finite number of vertices and edges.
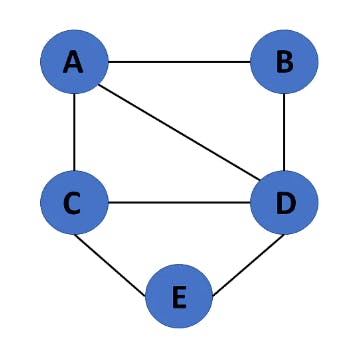
13. Connected Graph
If there is a path between one vertex of a graph data structure and any other vertex, the graph is connected.
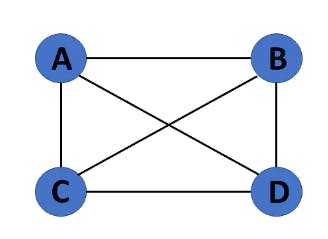
14. Disconnected Graph
When there is no edge linking the vertices, you refer to the null graph as a disconnected graph.
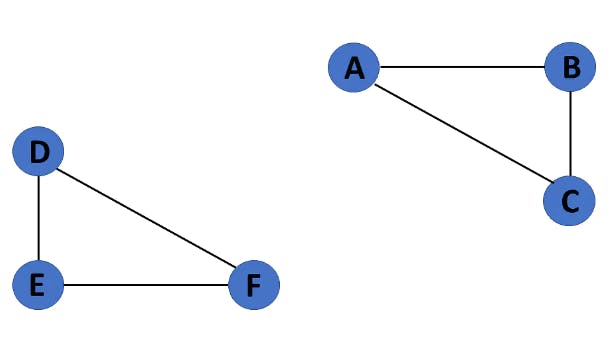
15. Cyclic Graph
If a graph contains at least one graph cycle, it is considered to be cyclic.
16. Acyclic Graph
When there are no cycles in a graph, it is called an acyclic graph.
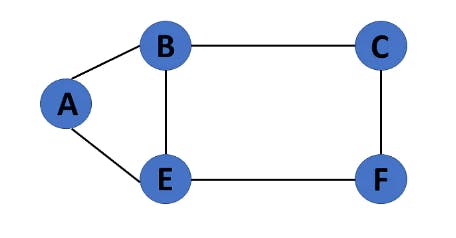
17. Directed Acyclic Graph
It's also known as a directed acyclic graph (DAG), and it's a graph with directed edges but no cycle. It represents the edges using an ordered pair of vertices since it directs them and stores some data.
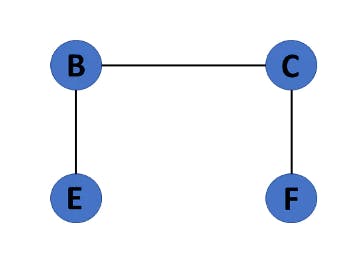
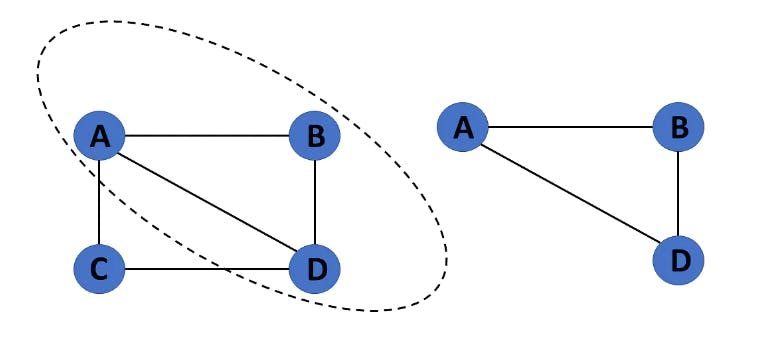
18. Subgraph
The vertices and edges of a graph that are subsets of another graph are known as a subgraph.
Terminologies of Graph data structure
- The total number of edges occurring to a vertex in a graph is its degree.
- The out-degree of a vertex in a directed graph is the total number of outgoing edges, whereas the in-degree is the total number of incoming edges.
- A vertex with an in-degree of zero is referred to as a source vertex, while one with an out-degree of zero is known as a sink vertex.
- A path is a set of alternating vertices and edges, with each vertex connected by an edge.
- The path that starts and finishes at the same vertex is known as a cycle.
- For each pair of vertices x and y, a graph is strongly connected if it contains a directed path from x to y and a directed path from y to x.
Graph representation in data structure
The most frequent graph representations are the two that follow:
- Adjacency matrix
- Adjacency list
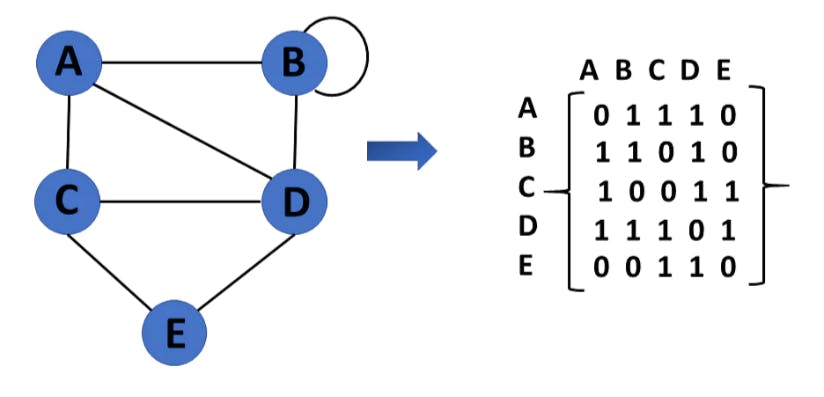
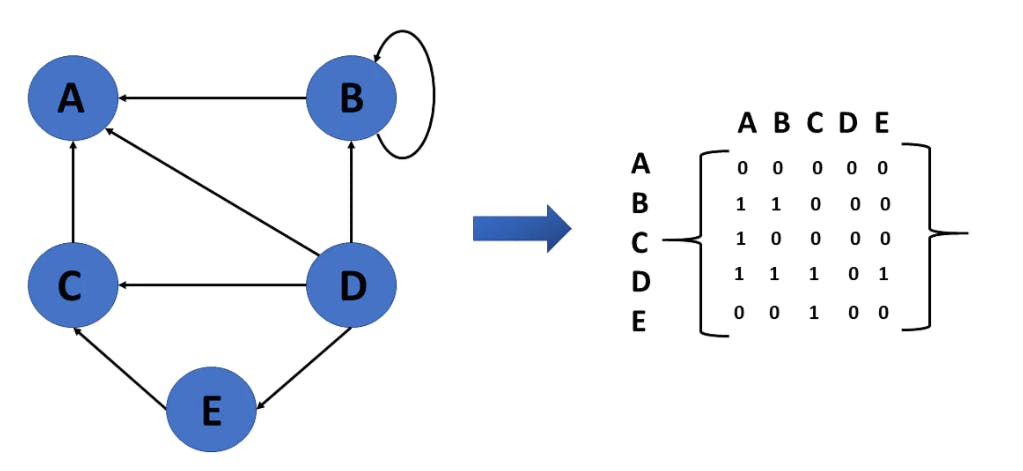
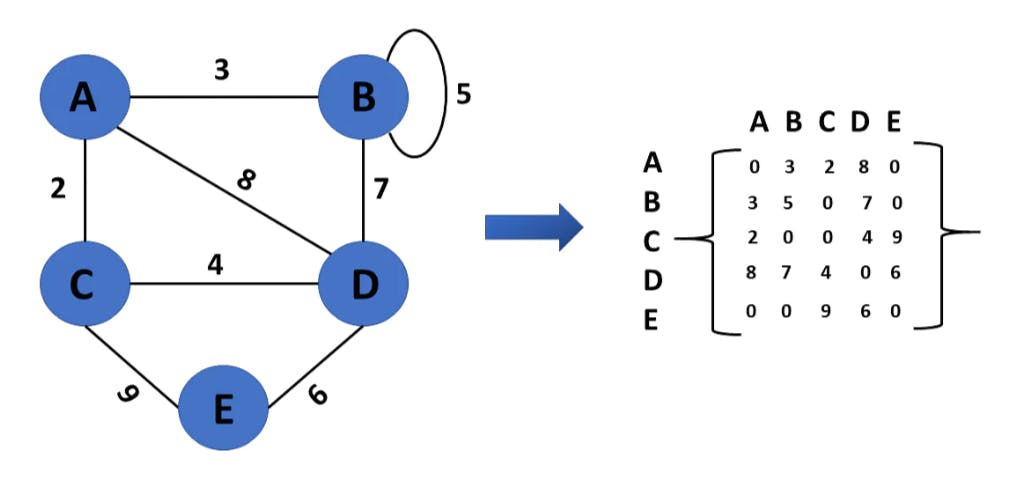
Adjacency matrix
🔸A sequential representation is an adjacency matrix.
🔸It's used to show which nodes are next to one another. I.e., is there any connection between nodes in a graph?
🔸You create an MXM matrix G for this representation. If an edge exists between vertex a and vertex b, the corresponding element of G, gi,j = 1, otherwise gi,j = 0.
🔸If there is a weighted graph, you can record the edge's weight instead of 1s and 0s.
Example representation -
Undirected graph:
Directed graph:
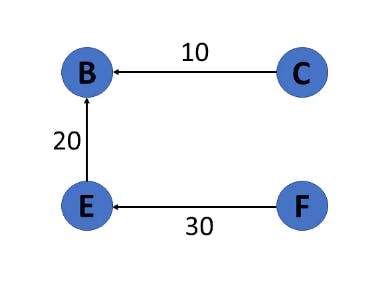
Weighted undirected graph:
Weight or cost is indicated at the graph's edge, a weighted graph representing these values in the matrix.
Java code for adjacency matrix representation of an undirected graph -
// Adjacency Matrix representation in Java
public class Graph {
private boolean adjMatrix[][];
private int numVertices;
// Initialize the matrix
public Graph(int numVertices) {
this.numVertices = numVertices;
adjMatrix = new boolean[numVertices][numVertices];
}
// Add edges
public void addEdge(int i, int j) {
adjMatrix[i][j] = true;
adjMatrix[j][i] = true;
}
// Remove edges
public void removeEdge(int i, int j) {
adjMatrix[i][j] = false;
adjMatrix[j][i] = false;
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
}
}
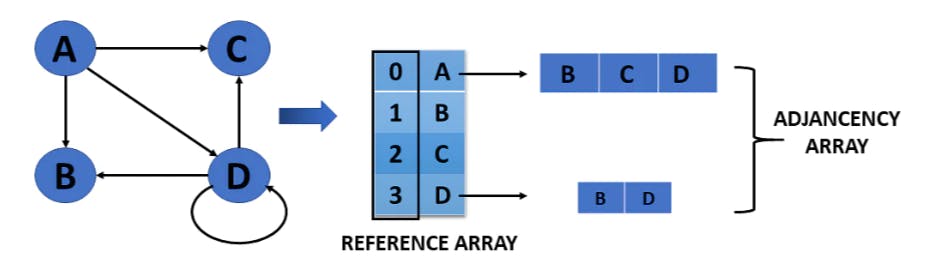
Adjacency List
🔸A linked representation is an adjacency list.
🔸You keep a list of neighbors for each vertex in the graph in this representation. Each vertex in the graph has a list of its neighboring vertices.
🔸You have an array of vertices indexed by the vertex number, and the corresponding array member for each vertex x points to a singly linked list of x's neighbors.
Undirected Graph Representation Using Linked-List:
Undirected Graph Representation Using an Array:
Java code for adjacency list representation of a graph -
public static void main (String[] args) {
int n = 3; // no of vertices
ArrayList<ArrayList<Integer> > adj = new ArrayList<ArrayList<Integer> >();
for (int i = 0; i <= n; i++)
adj.add(new ArrayList<Integer>());
// Basic syntax -
// adj.get(u).add(v);
// adj.get(v).add(u);
}
Creating graphs
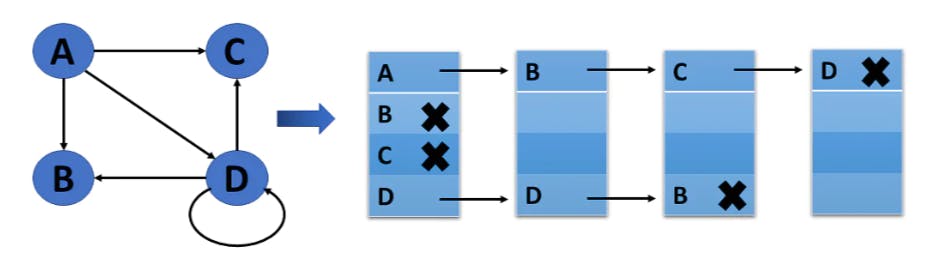
Insert vetrex
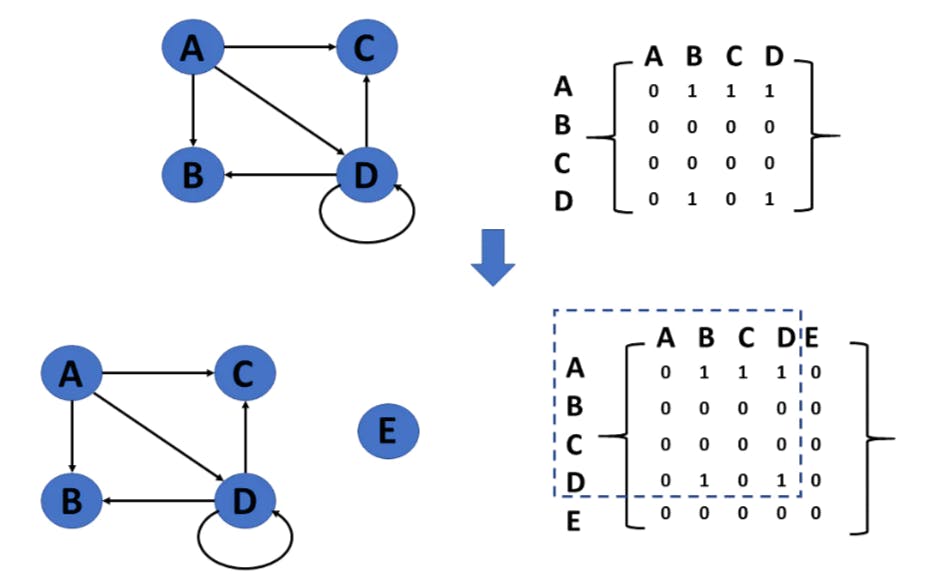
Delete vertex
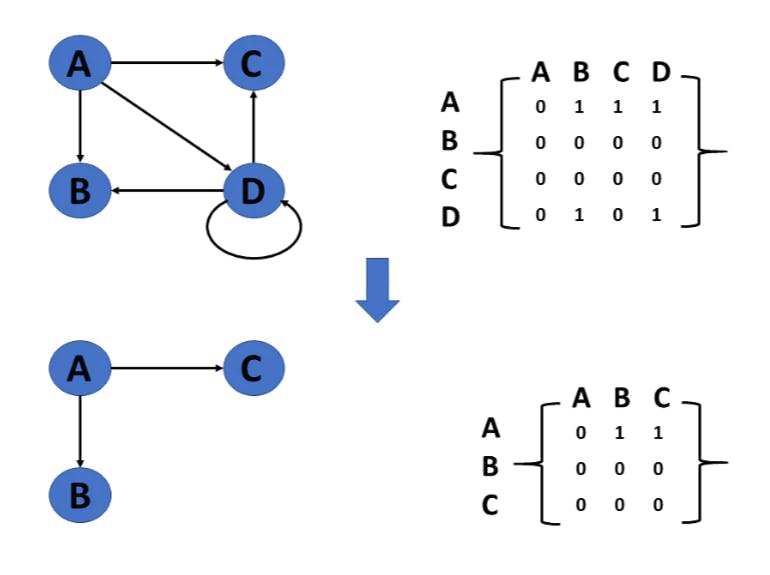
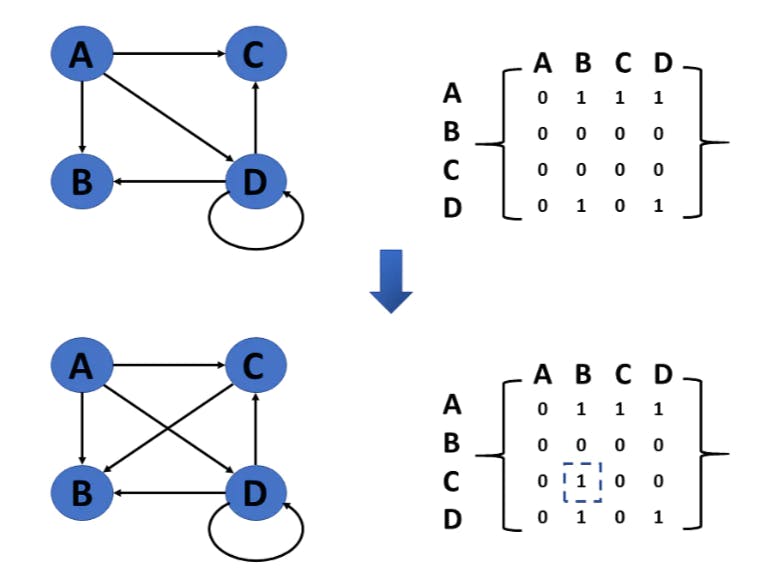
Insert edge
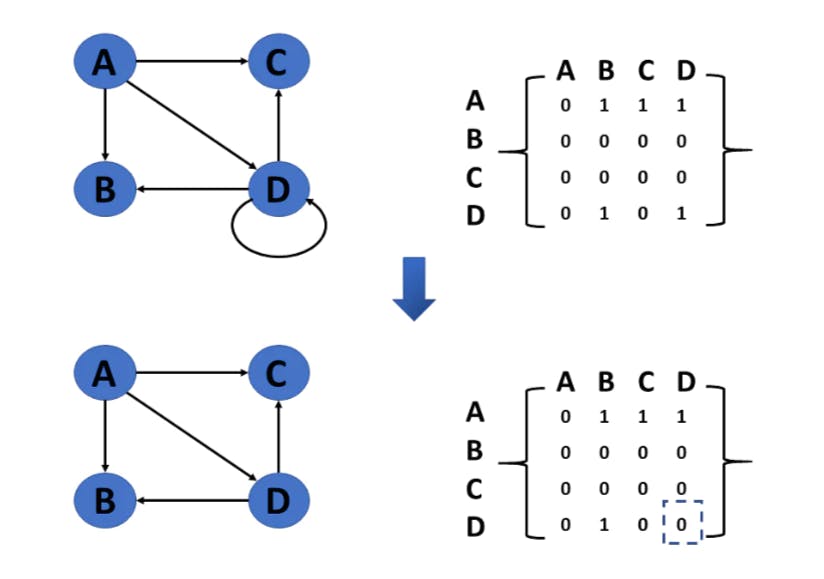
Delete edge
Graph Traversals
Breadth First Search (BFS)
It begins at the root of the graph and investigates all nodes at the current depth level before moving on to nodes at the next depth level.
To maintain track of the child nodes that have been encountered but not yet inspected, more memory, generally you require a queue.
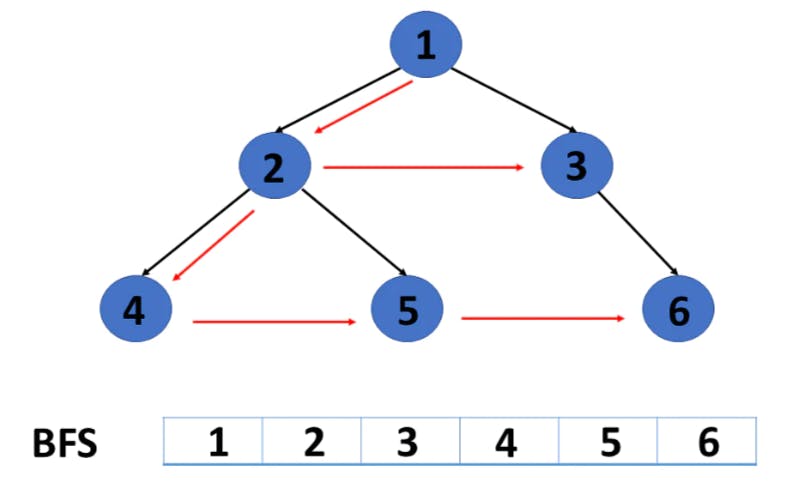
Java code for BFS of a graph -
// Time complexity: O(V+E)
// Space complexity: O(V+E) + O(V) + O(V)
// Space for adjacency list, visited array, queue data structure
public static ArrayList<Integer> bfsOfGraph(int V,ArrayList<ArrayList<Integer>> adj) {
ArrayList<Integer> bfs = new ArrayList<>();
boolean vis[] = new boolean[V];
Queue<Integer> q = new LinkedList<>();
q.add(0);
vis[0] = true;
while (!q.isEmpty()) {
Integer node = q.poll();
bfs.add(node);
// Get all adjacent vertices of the dequeued vertex s
// If a adjacent has not been visited, then mark it
// visited and enqueue it
for (Integer it: adj.get(node)) {
if (vis[it] == false) {
vis[it] = true;
q.add(it);
}
}
}
return bfs;
}
Depth First Search (DFS)
The depth-first search (DFS) algorithm traverses or explores data structures such as trees and graphs. The DFS algorithm begins at the root node and examines each branch as far as feasible before backtracking.
To maintain track of the child nodes that have been encountered but not yet inspected, more memory, generally a stack, is required.
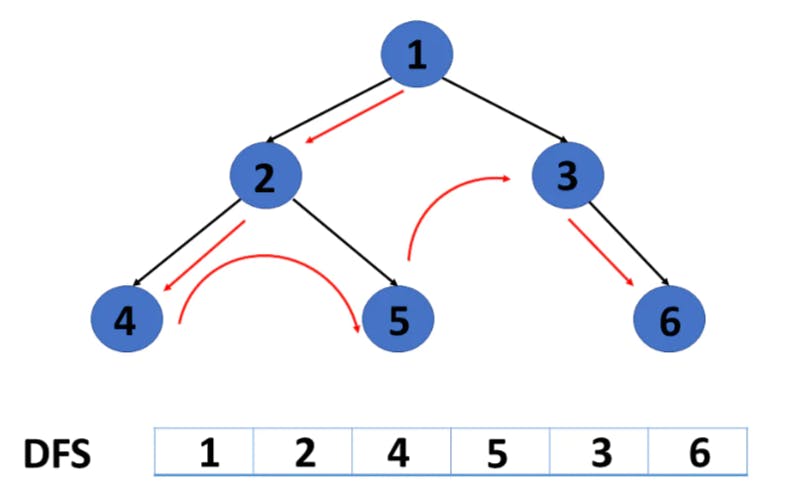
Java code for DFS of a graph -
// Time complexity: O(V+E)
// Space complexity: O(V+E) + O(V) + O(V)
// Space for adjacency list, Array,Auxiliary space
public static void dfs(int node, boolean vis[], ArrayList<ArrayList<Integer>> adj, ArrayList<Integer> storeDfs) {
storeDfs.add(node);
//marking current node as visited
vis[node] = true;
//getting neighbour nodes
for(Integer it: adj.get(node)) {
if(vis[it] == false) {
dfs(it, vis, adj, storeDfs);
}
}
}
public static ArrayList<Integer> dfsOfGraph(int V, ArrayList<ArrayList<Integer>> adj)
{
ArrayList<Integer> storeDfs = new ArrayList<>();
//boolean array to keep track of visited vertices
boolean vis[] = new boolean[V];
//If you are starting from node 2, then i should start from 2.
for(int i=0;i<V;i++) {
if(!vis[i])
dfs(i, vis, adj, storeDfs);
}
return storeDfs;
}
Connected components in an undirected graph
The following graph contains three connected components-
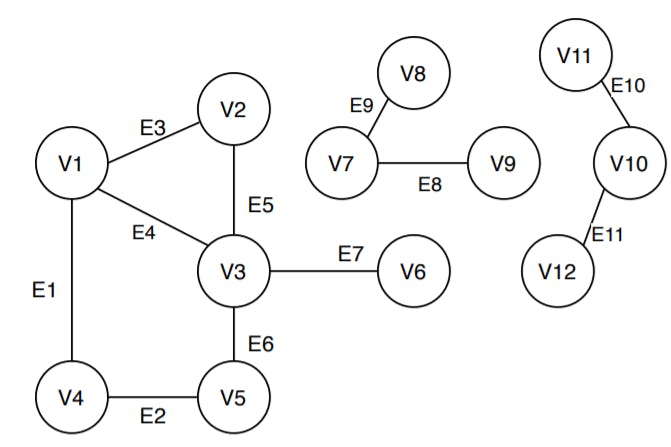
// Algorithm
Component_count = 0
for each vertex k in V:
visited[k]=false
for each vertex k in V:
if (visited[k]==false)
DFS(visited,k) OR BFS(visited,k)
Component_count++
Cycle detection in an undirected graph
Using BFS -
class Node {
int curr;
int parent;
Node(int curr,int parent) {
this.curr=curr;
this.parent=parent;
}
}
class cycleDetectInGraph {
// Function to detect cycle in an undirected graph.
public boolean isCycle(int V, ArrayList<ArrayList<Integer>> adj) {
boolean[] visited = new boolean[V];
for (int i=0;i<V;i++) {
if (!visited[i]) {
if (checkCycle(adj,visited,i))
return true;
}
}
return false;
}
private boolean checkCycle(ArrayList<ArrayList<Integer>> adj,
boolean[] visited, int v) {
// BFS
Queue<Node> q=new LinkedList<>();
q.add(new Node(v,-1));
visited[v]=true;
while (!q.isEmpty()) {
Node current = q.poll();
for (int i: adj.get(current.curr)) {
if (!visited[i]) {
q.add(new Node(i,current.curr));
visited[i]=true;
}
else if (i!=current.parent) {
// Cycle exists
return true;
}
}
}
return false;
}
}
Using DFS -
// 0-based indexing Graph
public boolean isCycle(int V, ArrayList<ArrayList<Integer>> adj) {
boolean vis[] = new boolean[V];
for (int i = 0; i < V; i++) {
if (vis[i] == false) {
if (checkForCycle(i, -1, vis, adj))
return true;
}
}
return false;
}
public boolean checkForCycle(int node,int parent,boolean vis[],ArrayList<ArrayList<Integer>> adj) {
vis[node] = true;
for (Integer it: adj.get(node)) {
if (vis[it] == false) {
if (checkForCycle(it, node, vis, adj) == true)
return true;
} else if (it != parent) {
// If the previously visited node and it is not equal to the parent
// we can say there is cycle
return true;
}
}
return false;
}
Cycle detection in a directed graph
public boolean isCyclic(int V, ArrayList<ArrayList<Integer>> adj) {
boolean[] visited = new boolean[V];
boolean[] dfsVisit = new boolean[V];
for (int i=0;i<V;i++) {
if (!visited[i]) {
if (checkCycle(adj,visited,dfsVisit,i))
return true;
}
}
return false;
}
private boolean checkCycle(ArrayList<ArrayList<Integer>> adj,
boolean[] visited, boolean[] dfsVisit, int v) {
// DFS
visited[v]=true;
dfsVisit[v]=true;
for (int i: adj.get(v)) {
if (!visited[i]) {
if (checkCycle(adj,visited,dfsVisit,i))
return true;
}
else if (dfsVisit[i]) {
// If visited node as well as present in dfsVisit- cycle exists
return true;
}
}
dfsVisit[v]=false; // Mark false again while backtracking
return false;
}
Bipartite Graphs
A graph G=(V, E) is called a bipartite graph if its vertices V can be partitioned into two subsets V₁ and V₂ such that each edge of G connects a vertex of V₁ to a vertex V₂. It is denoted by Kₘₙ, where m and n are the numbers of vertices in V₁ and V₂ respectively.
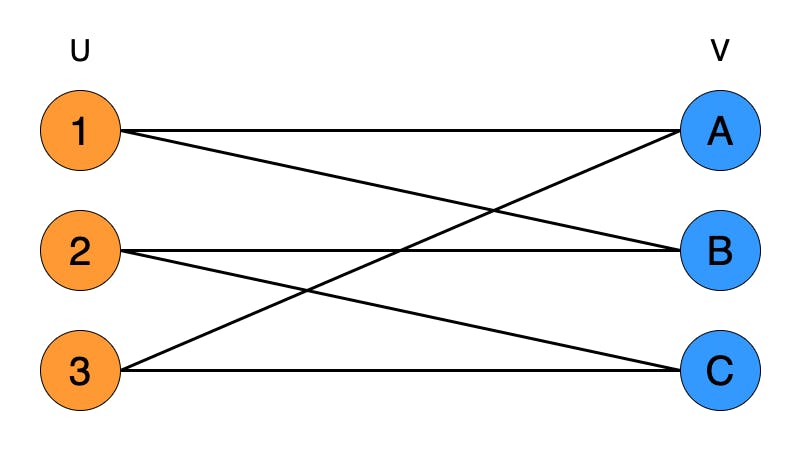
Using DFS -
public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] color = new int[n];
Arrays.fill(color,-1); // No color
for (int i=0;i<n;i++) {
if (color[i]==-1 && !bipartiteDFS(graph,color,i))
return false;
}
return true;
}
private boolean bipartiteDFS(int[][] graph,int[] color,int node) {
if (color[node]==-1) {
color[node]=1;
}
for (int neighbor: graph[node]) {
if (color[neighbor]==-1) {
// Neighbor not colored yet - Color opposite color
color[neighbor]=1-color[node];
if (!bipartiteDFS(graph,color,neighbor))
return false;
}
else if (color[neighbor]==color[node]) {
// Same color to neighbor- not bipartite
return false;
}
}
return true;
}
Using BFS -
public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] color = new int[n];
Arrays.fill(color,-1); // No color
for (int i=0;i<n;i++) {
if (color[i]==-1 && !bipartiteBFS(graph,color,i))
return false;
}
return true;
}
private boolean bipartiteBFS(int[][] graph,int[] color,int node) {
Queue<Integer> q = new LinkedList<>();
q.add(node);
color[node]=1; // First color-1 and second color-0
while (!q.isEmpty()) {
int curr = q.poll();
// Get neighbors of curr
for (int neighbor: graph[curr]) {
if (color[neighbor]==-1) {
// Neighbor not colored yet - Color opposite color
color[neighbor]=1-color[curr];
q.add(neighbor);
}
else if (color[neighbor]==color[curr]) {
// Same color to neighbor- not bipartite
return false;
}
}
}
return true;
}
Topological sort
Topological sorting of vertices of a Directed Acyclic Graph is an ordering of the vertices v₁,v₂,v₃,.....,vₙ in such a way, that if there is an edge directed towards vertex vⱼ from vertex vᵢ, then vᵢ comes before vⱼ. For example, consider the graph given below:
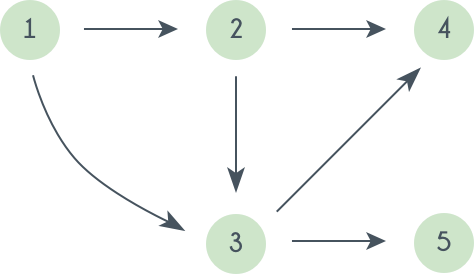
The topological sorting of this graph is: 1 2 3 4 5
There are multiple topological sorting possible for a graph. For the graph given above one another topological sorting is: 1 2 3 5 4
In order to have a topological sorting, the graph must not contain any cycles.
Using DFS -
static int[] topoSort(int V, ArrayList<ArrayList<Integer>> adj)
{
Stack<Integer> st = new Stack<>();
boolean[] visited = new boolean[V];
for (int i=0;i<V;i++) {
if (!visited[i]) {
findTopoSort(adj,st,visited,i);
}
}
// Stack contains the topo sort
int[] topo = new int[V];
int index=0;
while (!st.isEmpty()) {
topo[index++]=st.pop();
}
return topo;
}
// Topological sort using DFS
private static void findTopoSort(ArrayList<ArrayList<Integer>> adj, Stack<Integer> st,
boolean[] visited, int node) {
visited[node]=true;
for (int neighbor: adj.get(node)) {
if (!visited[neighbor]) {
findTopoSort(adj,st,visited,neighbor);
}
}
st.push(node);
}
Kahn's algorithm (Using BFS) -
static int[] topoSort(int V, ArrayList<ArrayList<Integer>> adj)
{
Queue<Integer> q = new LinkedList<>();
int[] indegree = new int[V];
for (int i=0;i<V;i++) {
for (int neigh: adj.get(i))
indegree[neigh]++;
}
// Add vertices with indegree 0 to queue
for (int i=0;i<V;i++) {
if (indegree[i]==0)
q.add(i);
}
// To store topo sort
int[] topo = new int[V];
int index = 0;
while (!q.isEmpty()) {
int curr = q.poll();
topo[index++]=curr;
for (int neighbor: adj.get(curr)) {
indegree[neighbor]--;
if (indegree[neighbor]==0)
q.add(neighbor);
}
}
return topo;
}
Cycle detection in a directed graph using BFS
In Kahn's algorithm,
// Algorithm
Find topo sort using BFS and maintain count of elements in topo sort yet
if (count==no Of vertices)
return false; // Not cyclic
return true; // Is cyclic
Shortest path in an undirected graph with unit weights
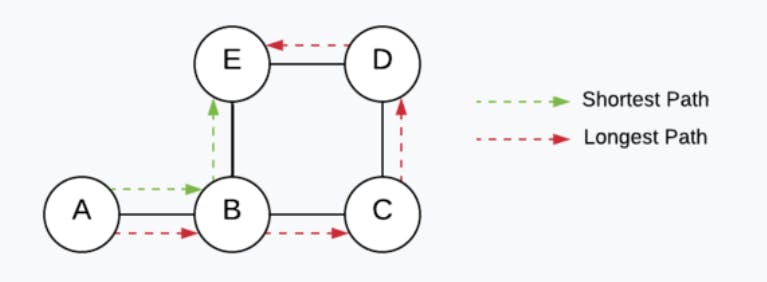
Java code -
// Using BFS
private void shortestPath(ArrayList<ArrayList<Integer>> adj,int N,int src)
{
int[] dist = new int[N];
for(int i=0;i<N;i++)
dist[i]=1000000000; // Set distance to infinity initially
Queue<Integer> q=new LinkedList<>();
dist[src]=0;
q.add(src);
while(!q.isEmpty())
{
int node = q.poll();
for(int it:adj.get(node)){
if(dist[node]+1<dist[it]){
dist[it]=dist[node]+1;
q.add(it);
}
}
}
// Print shortest distance of source with each node
for(int i=0;i<N;i++) {
System.out.print(dist[i]+" ");
}
}
Shortest path in Directed Acyclic Graph (DAG)
Algorithm:
- Find the topological ordering of the given graph
- Create an array(say dist) of size V, and initialize all its entries with a very large number (say INF).
- Traverse over all the vertices in topological order and for each vertex u, check the following conditon for all the adjancent vetex v of u If ( dist[v] > dist[u] + weightOfEdge(u→v)) then dist[v] =dist[u] + weightOfEdge(u→v)
Consider the below given Directed acyclic graph and let's say we need to find the shortest distance of all vertices from vertex 0.
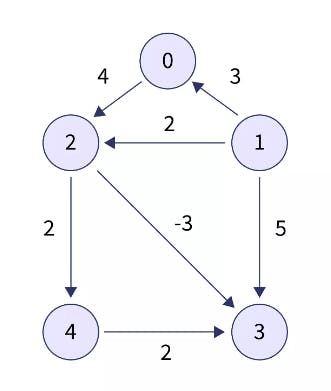
As per the algorithm discussed, we will first find the topological sorting of this graph. topo = [1, 0, 2, 4, 3]
Now we will create an array dist of size V (here V=5) all entries of which will be initialized with INF. Then assign dist[start]=0. dist = [0, INF, INF, INF, INF]
The next step is to traverse vertices in topological order.
topo[0]=1
The adjacent vertices of 1 are 0, 2, and 3. So we will check the following:
🔸If dist[0] > dist[1] + weightOfEdge(1 → 0), putting their values will give 0 > INF + 3, which evaluates to false.
🔸If dist[2] > dist[1] + wightOfEdge(1 → 2), putting their values will give INF > INF + 2, which evaluates to false.
🔸If dist[3] > dist[1] + wightOfEdge(1 → 3), putting ther values will give INF > INF + 5, which evaluates to false. After these steps dist array will look like dist = [0, INF, INF, INF, INF]topo[1]=0
The adjacent vertex of 0 is 2. So we will check the following:
🔸If dist[2] > dist[0] + weightOfEdge(0 → 2) putting their values will give INF > 0 + 4, which evaluates to true hence we will assign 4 to dist[2]. After this step dist array will look like dist = [0, INF, 4, INF, INF]topo[2]=2
The adjacent vertices of 2 are 3 and 4. So we will check the following:
🔸If dist[3] > dist[2] + weightOfEdge(2 \rightarrow→ 3), putting their values will give INF > 4 + (-3), which evaluates to true hence we will assign 1 to dist[3].
🔸If dist[4] > dist[2] + weightOfEdge(2 \rightarrow→ 4), putting their values will give INF > 4 + 2, which evaluates to true hence we will assign 6 to dist[4]. After these steps dist array will look like dist = [0, INF, 4, 1, 6]topo[3]=4
The adjacent vertex of 4 is 3. So we will check the following:
🔸If dist[3] > dist[4] + weightOfEdge(4 → 3) putting their values will give 1 > 6 + 2, which evaluates to false.topo[4]=3
There are no adjacent vertices to 3 hence we will not do anything.
Finally the dist array will be dist=[0, INF, 4, 1 ,6].
Java code -
class ShortestPathInDAG
{
int V; // No of vertices
int INF=Integer.MAX_VALUE; // Infinity
class Node{
int v;
int wt;
Node(int v,int wt){
this.v=v;
this.wt=wt;
}
}
void topologicalSort(int v,boolean visited[],Stack<Integer> st){
visited[v]=true;
for(Node node:adj.get(v)){
if(!visited[node.v]){
topologicalSort(node.v, visited, st);
}
}
st.push(v);
}
// Time complexity - O(V+E)
// Space complexity - O(V)
void shortestPath(int src){
// To store the topological sort
Stack<Integer> st=new Stack<>();
int dist[]=new int[V];
Arrays.fill(dist,INF);
dist[src]=0;
boolean visited[]=new boolean[V];
for(int i=0;i<V;i++){
if(!visited[i]){
topologicalSort(i,visited,st);
}
}
// Iterate till the stack is not empty.
while(!st.isEmpty()){
int u=st.pop();
if(dist[u]!=INF){
for(Node node:adj.get(u)){
if(dist[node.v]>dist[u]+node.wt)
dist[node.v]=dist[u]+node.wt;
}
}
}
// Print distances with the src node
for(int i=0;i<V;i++){
if(dist[i]==INF)
System.out.print("INF ");
else
System.out.print(dist[i]+" ");
}
}
}
The intuition behind using topological sort:
Processing the vertices in topological order ensures that by the time you get to a vertex, you've already processed all the vertices that can precede it.Note:
The following algorithm cannot be applied for graphs that contain cycles.
Shortest path in undirected graph - Dijkstra Algorithm
class Node implements Comparable<Node> {
int val;
int wt;
Node(int val,int wt) {
this.val=val;
this.wt=wt;
}
// Ascending order of wts
public int compareTo(Node n) {
return this.wt-n.wt;
}
}
class Main
{
void shortestPath(int s,ArrayList<ArrayList<Node>> adj, int N)
{
int dist[] = new int[N];
for(int i=0;i<N;i++)
dist[i] = 100000000; //Infinity
dist[s]=0;
PriorityQueue<Node> pq = new PriorityQueue<Node>(N);
pq.add(new Node(s,0));
while(pq.size()>0) {
Node node = pq.poll();
for(Node it: adj.get(node.val())) {
if(dist[node.val()] + it.wt() < dist[it.val()]) {
dist[it.val()] = dist[node.val()] + it.wt();
pq.add(new Node(it.val(), dist[it.val()]));
}
}
}
System.out.println("The distances from source "+s+" are : ");
for (int i=0;i<N;i++)
{
System.out.print(dist[i]+" ");
}
}
}