1 byte = 8 bits.
Any integer or character can be represented using bits, which we call its binary form(contains only 1 or 0) or in its base 2 form.
Example:
14 = {1110}₂
= 1x2³ + 1x2² + 1x2¹ + 0x2⁰
= 14
For characters, we use ASCII representation, which is in the form of integers which again can be represented using bits.
Bitwise Operators
There are different bitwise operations used in bit manipulation. These bit operations operate on the individual bits of the bit patterns. Bit operations are fast and can be used in optimizing time complexity. Some common bit operators are:
Bitwise NOT (~)
Bitwise NOT is a unary operator that flips the bits of the number i.e., if the ith bit is 0, it will change it to 1 and vice versa. Bitwise NOT is nothing but simply the one’s complement of a number.
Bitwise AND (&)
Bitwise AND is a binary operator that operates on two equal-length bit patterns. If both bits in the compared position of the bit patterns are 1, the bit in the resulting bit pattern is 1, otherwise 0.
To get the last bit of a number n, we simply Bitwise And it with 1 i.e (n&1) gives the last bit of a number.
Bitwise OR (|)
Bitwise OR is also a binary operator that operates on two equal-length bit patterns, similar to bitwise AND. If both bits in the compared position of the bit patterns are 0, the bit in the resulting bit pattern is 0, otherwise 1.
Bitwise XOR (^)
Bitwise XOR also takes two equal-length bit patterns. If both bits in the compared position of bit patterns are 0 or 1, the bit in the resulting bit pattern is 0, otherwise 1.
Properties of XOR:
- XOR of a number with itself is always 0
- XOR of a number with 0 is the number itself
- If a^b=c then c^a=b and b^c=a

Example:
int a = 5; // Binary representation: 101
int b = 6; // Binary representation: 110
System.out.println(a&b); // 100 i.e 4
System.out.println(a|b); // 111 i.e 7
System.out.println(a^b); // 011 i.e 3
Shift Operators
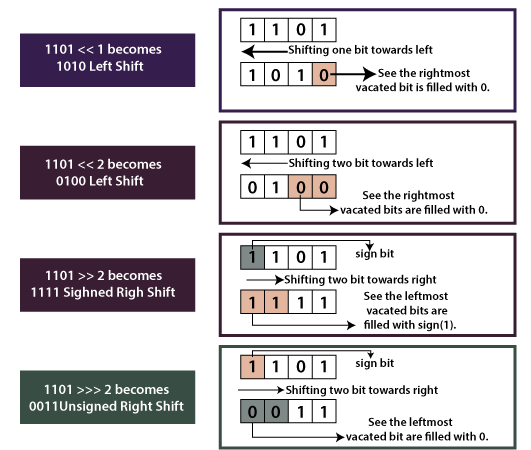
Left Shift (<<)
The left shift operator is a binary operator which shifts some number of bits, in the given bit pattern, to the left and appends 0 at the end. Left shift is equivalent to multiplying the bit pattern with 2ᵏ ( if we are shifting k bits ).
a=a<<1 is equivalent to a=a*2
Example:
int a = 5; // 0101
int b = a<<1; // 1010 i.e 10
int c = a<<2; //10100 i.e 20
Right Shift (>>)
The right shift operator is a binary operator which shifts some number of bits, in the given bit pattern, to the right and appends 0 at the other end if the number is positive and appends 1 if the number is negative. The right shift is equivalent to dividing the bit pattern with 2ᵏ ( if we are shifting k bits ).
a=a>>1 is equivalent to a=a/2
Example:
int a = 10; // 1010
int b = a>>1; // 0101 i.e 5
int c = a>>2; // 0010 i.e 2
Unsigned Right Shift (>>>)
The unsigned right-shift operator is a special type of right-shift operator that doesn't use the sign bit for filling the trailing position. The unsigned right-shift operator always fills the trialing position by 0.
Concept of mask
Left shift the number 1 i times to get the mask. Mask sets the ith bit (from right starting with 0) as 1 and the rest as 0.
mask = 1<<i;
// Example: 1<<2 is 100
Problems
Find a unique number in a list
Given a list of numbers in which there contains one number occurring only once and rest all numbers are repeated. You need to find that unique number.
We can simply XOR all the numbers and the result is the unique number. This works because XOR of a number with itself is 0 i.e
a^b^c^a^c = b
for (int i=0;i<n;i++) {
ans = ans^list[i]; // XOR of ans with list[i]
}
System.out.println("Answer is: "+ans);
Find whether a given number is even or odd
We can clearly say that if the last bit of a number is 1 it is odd and vice versa.
If the bitwise and of a number with 1 i.e number&1 is 1, it is odd and if it is 0 then it is even.
public static boolean isEven(int num) {
return (num&1)==1 ? false : true;
}
// Note here (num&1)==1 is used and not num&1==1 because in Java the
// precedence of == operator is more than the & operator
Get the ith bit of a number (from right)
The bit positions are starting with 0 from the right i.e for the number 5 i.e 101
-the 0th bit is 1
-the 1st bit is 0
-the 2nd bit is 1
Get the mask with ith bit set as 1 and then Bitwise AND the given number with the mask to make all bits except the ith bit as zero to get a new number. Now if this new number is greater than 0, it means the ith bit was 1 in the given number and vice versa.
public static int getIthBit(int num,int i) {
int mask = 1<<i;
return (num&mask)>0 ? 1 : 0;
}
Set the ith bit of a number
We need to set the ith bit of a number as 1 and get the new number.
Get the mask and then Bitwise OR the given number with the mask which sets the ith bit the number.
public static int setIthBit(int num,int i) {
int mask = 1<<i;
return (num|mask);
}
Clear the ith bit of a number
In this case, we need to retain all bits except the ith bit i.e we can Bitwise AND the given number with a number in which all bits are set to 1 except the ith bit. The negation of the mask is a number in which ith bit is 0 and all other bits are set.
public static int clearIthBit(int num,int i) {
int mask = ~(1<<i);
return (num&mask);
}
Update the ith bit of a number with a given value
We first cleared the ith bit. We next calculated the vMask as follows and then Bitwise OR it with the cleared number to get the result.
// v is either 0 or 1
public static int updateIthBit(int num,int i,int v) {
// Clear ith bit first
int mask = ~(1<<i);
int clearedNum = (num&mask);
// vMask is number with ith bit set to v
int vMask = (v<<i);
return (clearedNum|vMask);
}
Clear the last i bits of a number
If you need a number with all ones in it, you can use ~0 or -1.
Here we need a mask with all the bits set to one except the last i bits. Hence, we create it using -1<<i. Then find the Bitwise AND of the given number with the mask.
public static int clearLastIBits(int num,int i) {
int mask = (-1<<i);
return (num&mask);
}
// Example: clearLastIBits(7,2) returns 4
Clear a range of bits from i to j
i and j are considered from the right and j>=i.
2ᵏ - 1 is a number having k no of bits set to 1 in the end and rest 0.
And (2ᵏ - 1) is equivalent to (1<<k)-1
Here, we need a mask with all the bits in the range i to j set as 0 and other bits set as 1. Then find the Bitwise AND of the given number with the mask.
// Here, j>=i
public static int clearRangeOfBits(int num,int i,int j) {
int a = -1<<(j+1); // Number with upto j bits set to 0 in the end and rest 1
int b = (1<<i) - 1; // Number with upto i bits set to 1 in the end and rest 0
int mask = (a|b);
return (num&mask);
}
// Example: clearRangeOfBits(31,1,3) returns 17
Check if a given number is the power of 2
The Bitwise AND of a 2 power number and its predecessor is 0.
//num>=0
public static boolean isPowerOfTwo(int num) {
if (num==0) return false;
return (num&(num-1))==0;
}
Find the number of set bits in a number
Method 1:
public static int countBits(int num) {
int ans = 0;
while (num>0) {
ans += (num&1); // Adding last bit
num = num>>1; // Right shift
}
return ans;
}
// Time complexity - O(logN)
// This is because in any number N we have approximately logN bits.
Method 2:
Subtracting 1 from a decimal number flips all the bits after the rightmost set bit(which is 1) including the rightmost set bit.
So if we subtract a number by 1 and do it bitwise & with itself (n & (n-1)), we unset the rightmost set bit. If we do n & (n-1) in a loop and count the number of times the loop executes, we get the set bit count.
public static int countBits(int num) {
int ans = 0;
while (num>0) {
num = num&(num-1); // Removes the last set bit
ans++;
}
return ans;
}
// Time complexity - O(number of set bits)
Method 3:
Using the inbuilt method in Java
public static int countBits(int num) {
return Integer.bitCount(num);
}
Decimal to Binary
public static String decimalToBinary(int num) {
String str="";
while (num>0) {
str = ((num&1)==1 ? '1':'0') + str;
num = num>>1; // Right shift by 1
}
return str;
}
Using the inbuilt method in Java
public static String decimalToBinary(int num) {
return Integer.toBinaryString(num);
}
Unique number 2
Given an array in which two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.
public int[] singleNumber(int[] nums) {
int num1=0,num2=0;
int xor=0; // represents xor of all numbers
for (int i=0;i<nums.length;i++) {
xor = xor^nums[i];
}
// Get the position of first set bit from right
int pos = 0;
int temp = xor;
while ((temp&1)!=1) {
temp = temp>>1;
pos++;
}
// Mask with pos bit set to 1
int mask = 1<<pos;
for (int i=0;i<nums.length;i++) {
if ((nums[i]&mask)>0)
num1 = num1^nums[i];
}
num2 = num1^xor;
return new int[]{num1,num2};
}
Unique number 3
Given an integer array where every element appears three times except for one, which appears exactly once. Find the single element and return it.
public int singleNumber(int[] nums) {
// 32 bit array to store the result in binary
int ansBinary[] = new int[32];
for (int i=0;i<nums.length;i++) {
int num = nums[i];
int j=0;
// Count all bits at all positions and update the count array i.e ansBinary
while (num!=0) {
int leftBit = (num&1);
ansBinary[j] += leftBit;
j++;
num = num>>>1; // Unsigned right shift to handle negative numbers too
}
}
// Every element in the array is either 3N or 3N+1
int ans = 0;
int pow = 1;
for (int i=0;i<32;i++) {
ansBinary[i] %= 3;
ans += ansBinary[i]*pow;
pow = pow<<1;
}
return ans;
}
Exponentiation
Calculate exponent a^n.
Consider the following example - 6⁵
6⁵ = 6¹⁰¹ = 6⁴6⁰6¹
This is because 101 = 2²x1 + 2¹x0 + 2⁰x1
public static int exponent(int a,int n) {
int ans = 1;
while (n>0) {
int last_bit = (n&1);
ans *= last_bit==1 ? a : 1;
a=a*a;
n=n>>1;
}
return ans;
}
// Time complexity - O(logN)
Find the largest power of 2 less than or equal to a given number
Idea: Change all the bits which are at the right side of the most significant digit, to 1.
Property: As we know that when all the bits of a number N are 1, then N must be equal to the 2ᵏ-1, where k is the number of bits in N.
Example:
Let’s say N = 21 = {10101}, here most significant bit is the 4th one. (counting from 0th digit) and so the answer should be 16.
So let us change all the right side bits of the most significant bit to 1. Now the number changes to
{11111} = 31 = 2 * 16 -1 = Y (let’s say).
Now the required answer is (Y+1)>>1 or (Y+1)/2.
Now the question arises here is how can we change all right side bits of the most significant bit to 1?
Let’s take the N as 16-bit integer and binary form of N is {1000000000000000}.
Here we have to change all the right side bits to 1.
Initially, we will copy that most significant bit to its adjacent right side by:
N = N | (N>>1).

As you can see, in the above diagram, after performing the operation, the rightmost bit has been copied to its adjacent place.
Now we will copy the 2 rightmost set bits to their adjacent right side.
N = N | (N>>2).

Now we will copy the 4 rightmost set bits to their adjacent right side.
N = N | (N>>4)

Now we will copy these 8 rightmost set bits to their adjacent right side.
N = N| (N>>8)
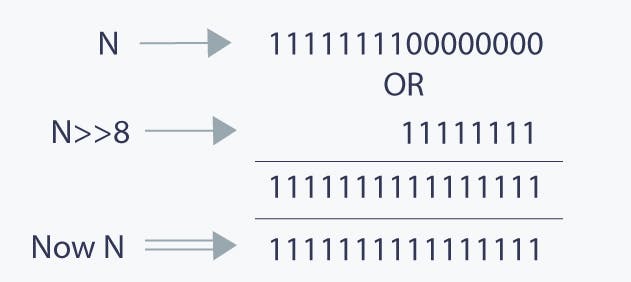
Now all the right side bits of the most significant set bit have been changed to 1. This is how we can change right side bits. This explanation is for a 16-bit integer, and it can be extended for a 32 or 64-bit integer too.
Implementation:
public static int largestPower(int n) {
//changing all right side bits to 1.
n = n | n>>1;
n = n | n>>2;
n = n | n>>4;
n = n | n>>8;
n = n | n>>16;
//as now the number is 2*x-1, where x is required answer, so adding 1 and dividing it by 2
return (n+1)>>1;
}
// Time complexity: O(1)
Note
x^(x&(x-1)) returns the rightmost 1 in binary representation of x.
x&(-x) returns the rightmost 1 in binary representation of x.
